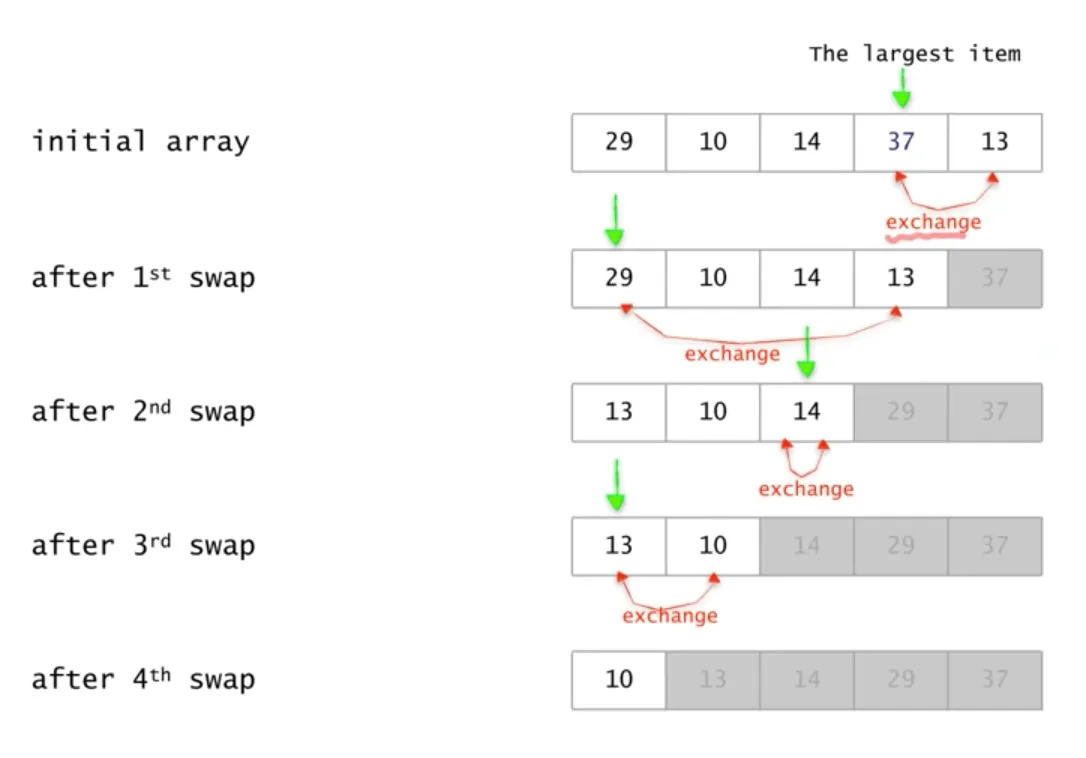
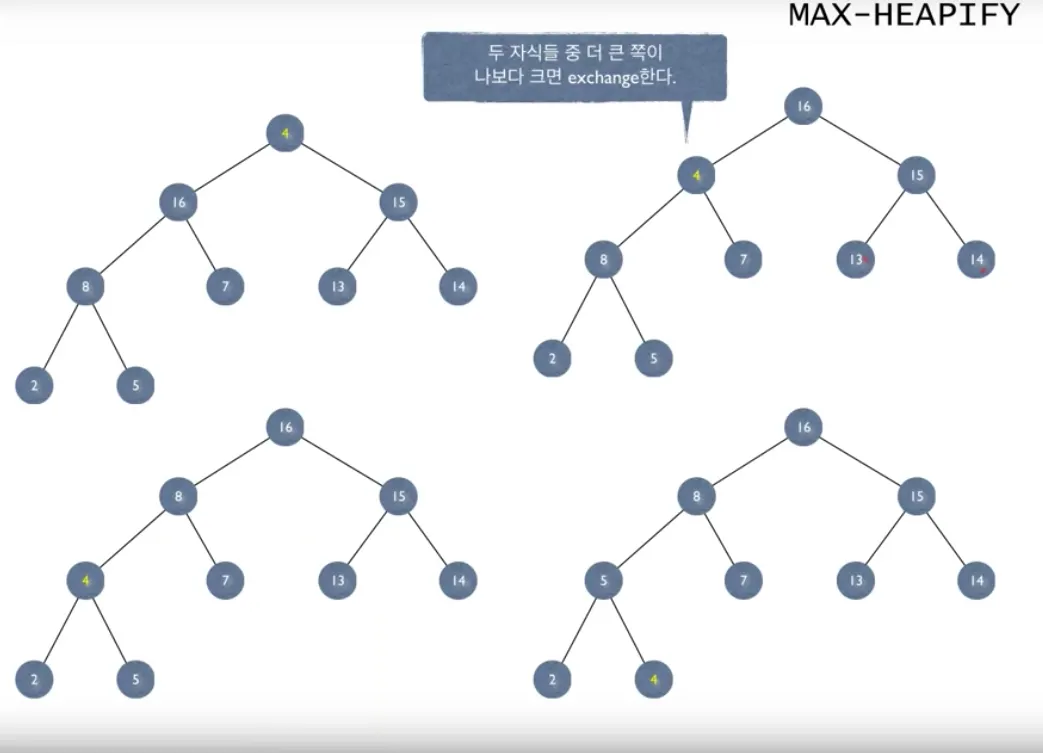
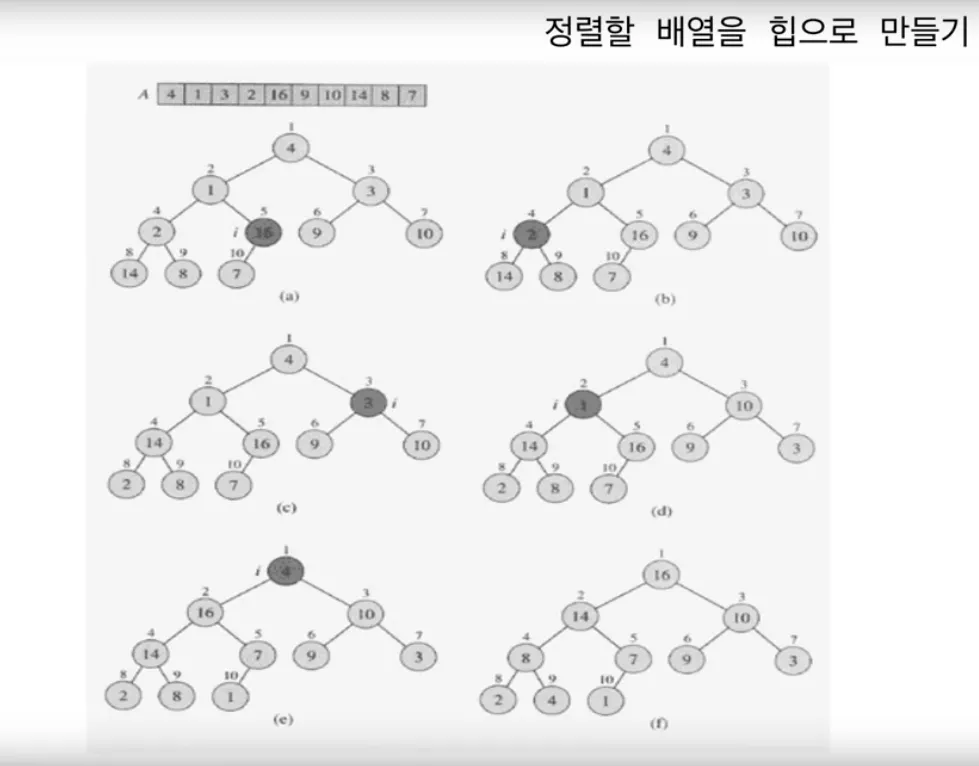
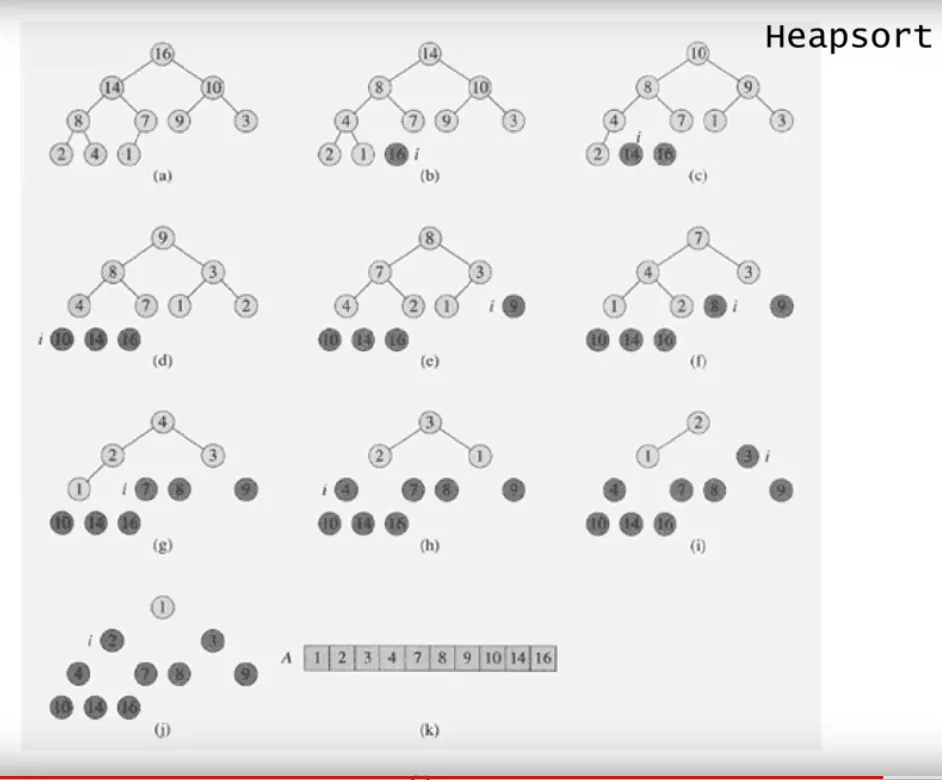
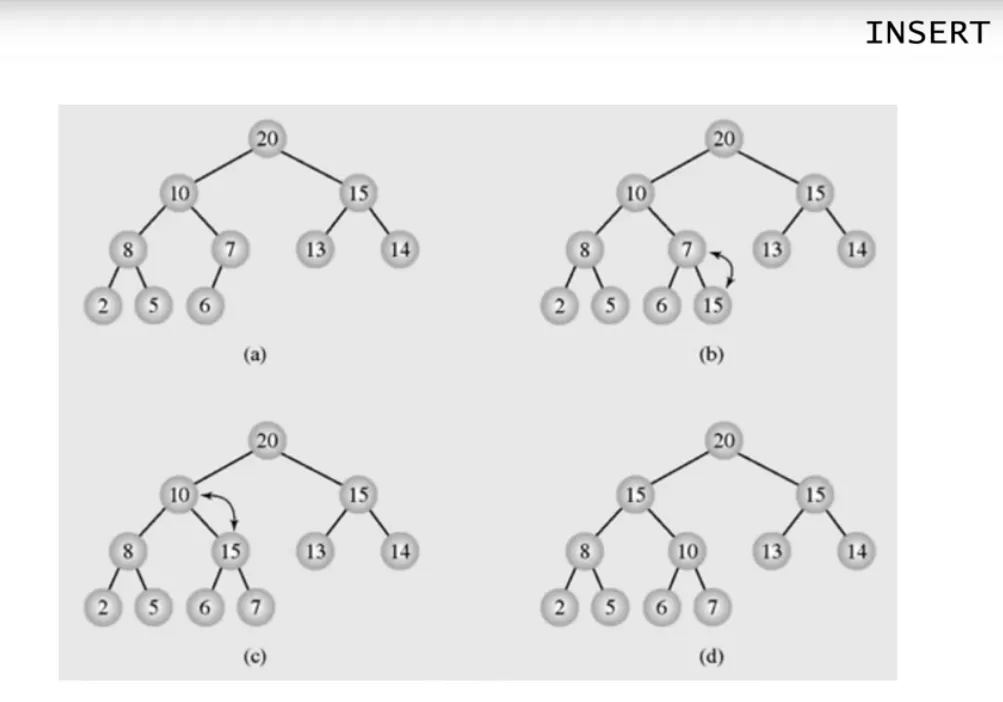
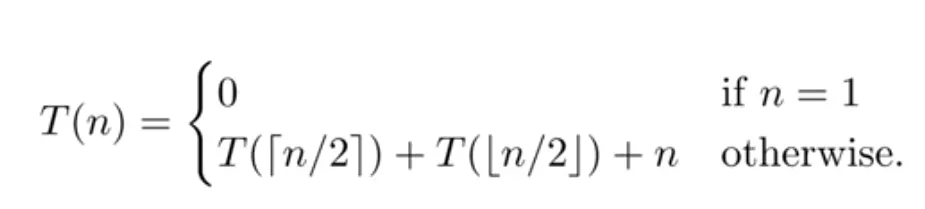Selection Sort
// 순차적으로 제일 큰 값들을 찾으면서 제일 마지막 자리와 변경 후 다음 제일 큰 숫자와 그 전 자리를 변경.
// 위 절차를 반복해서 정렬하는 정렬방식
// 시간복잡도 = T(n) = (n - 1) + (n - 2) + .... + 2 + 1 = O(n * n) = ((n*(n - 1))/2)
// 최악, 최선의 경우가 없이 항상 동일한 시간복잡도
JavaScript
복사
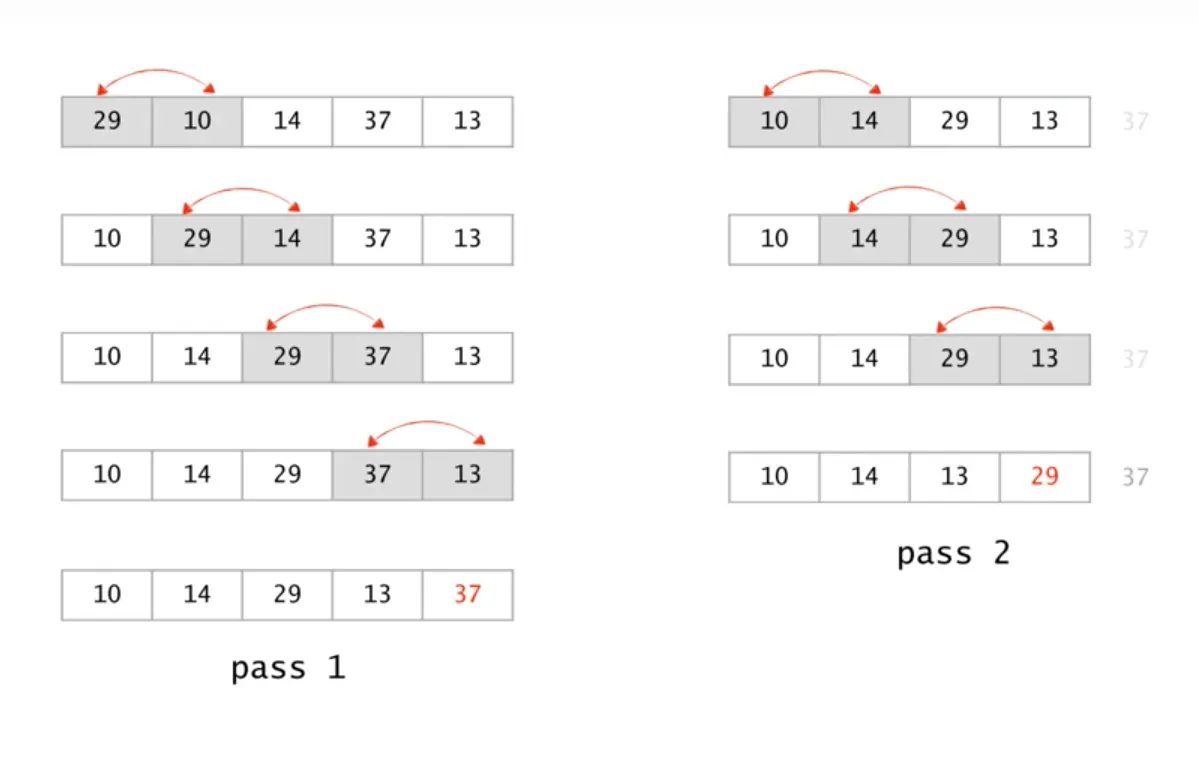
Bubble Sort
// 시간 복잡도 = T(n) = (n - 1) + (n - 2) + .... + 2 + 1 = O(n * n) = ((n*(n - 1))/2)
JavaScript
복사
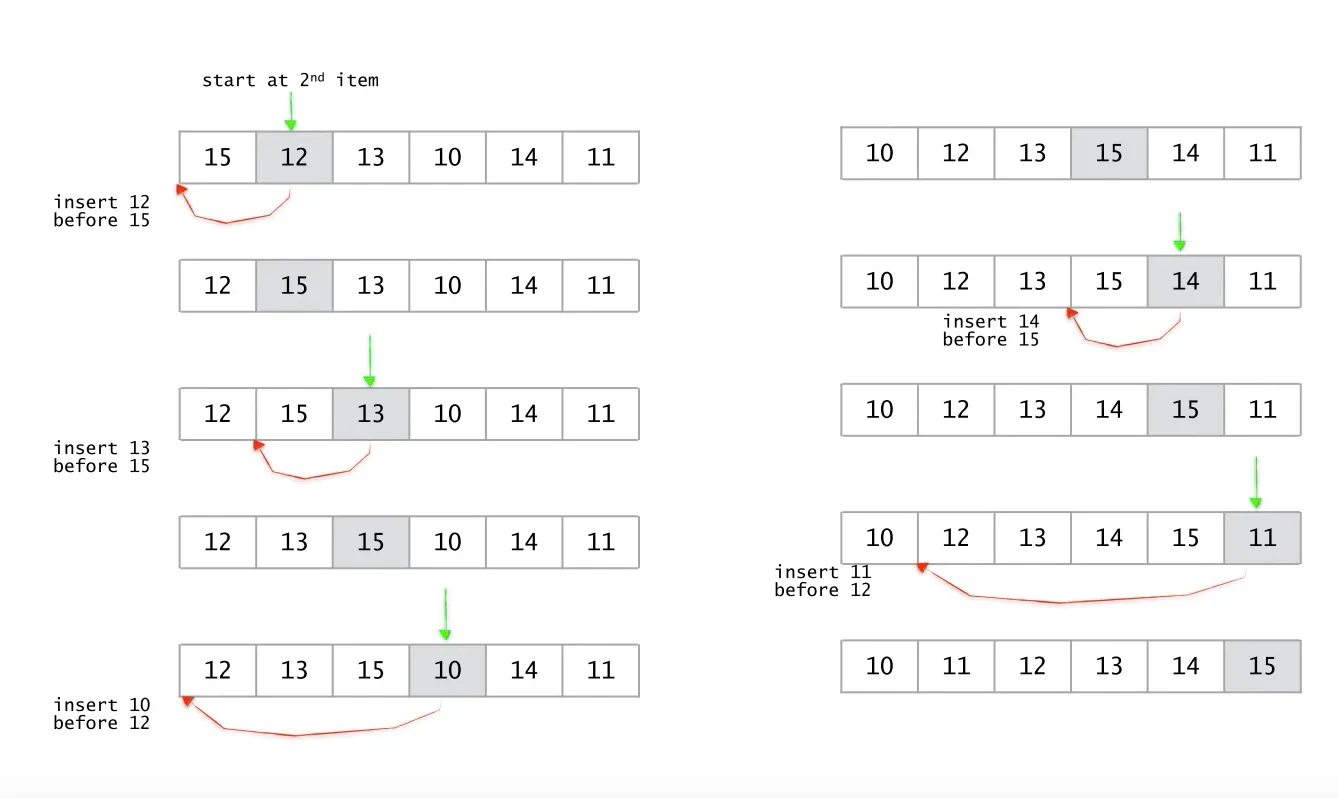
Insertion Sort
// 최악의 경우 T(n) = (n - 1) + (n - 2) + .... + 2 + 1 = O(n * n) = ((n*(n - 1))/2)
JavaScript
복사
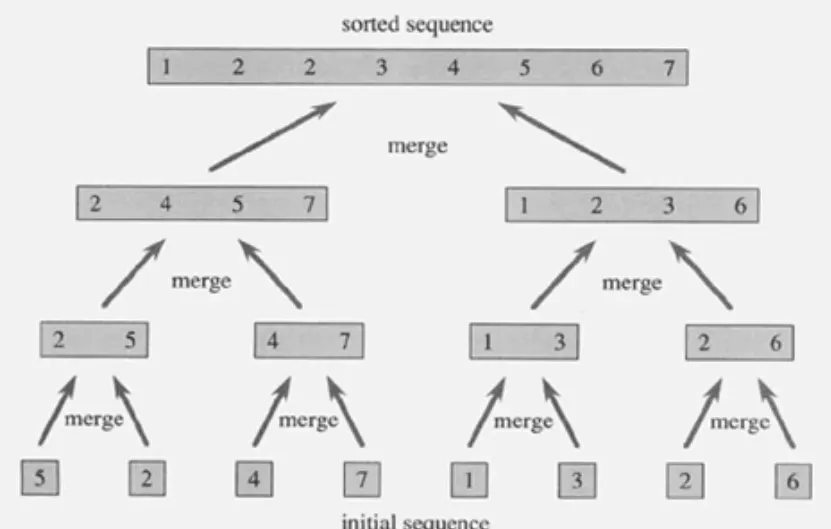
Merge Sort
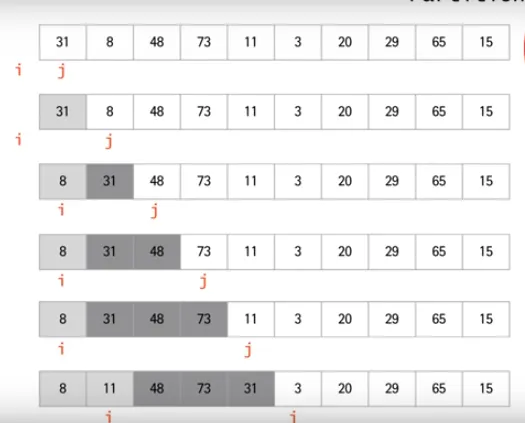
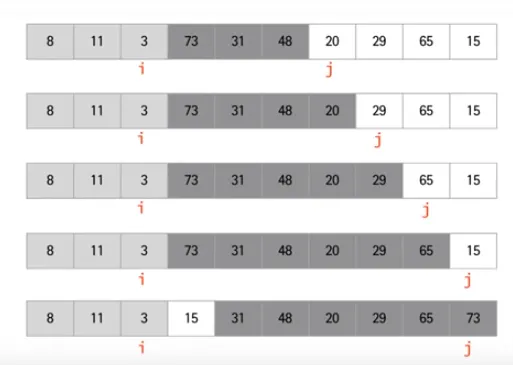
분할: 해결하고자 하는 문제를 작은 크기의 동일한 문제들로 분할
정복: 각각의 작은 문제를 순환적으로 해결
합병: 작은 문제의 해를 합하여 원래 문제에 대한 해를 구함
1.
데이터가 저장된 배열을 절반으로 나눔
2.
각각을 순환적으로 정렬
3.
정렬된 두개의 배열을 합쳐 전체 정렬
function mergeSort (list, p, r) {
if (q < r) {
var q = Math.floor((p + r) / 2);
mergeSort(A, p, q);
mergeSort(A, q + 1, r);
merge(A, p, q, r);
}
}
function merge (list, p, q, r) {
var i = p, j = q + 1, k = p;
var tmp = list.slice(0) // clone Array
while (i <= q && j <= r) {
if (list[i] <= data[j]) tmp[k++] = data[i++];
else tmp[k++] = data[j++];
}
while(i <= q) {
tmp[k++] = list[i++];
}
while(j <= r) {
tmp[k++] = list[j++];
}
for(var i = p; i <= r; i++) {
list[i] = tmp[i];
}
}
JavaScript
복사
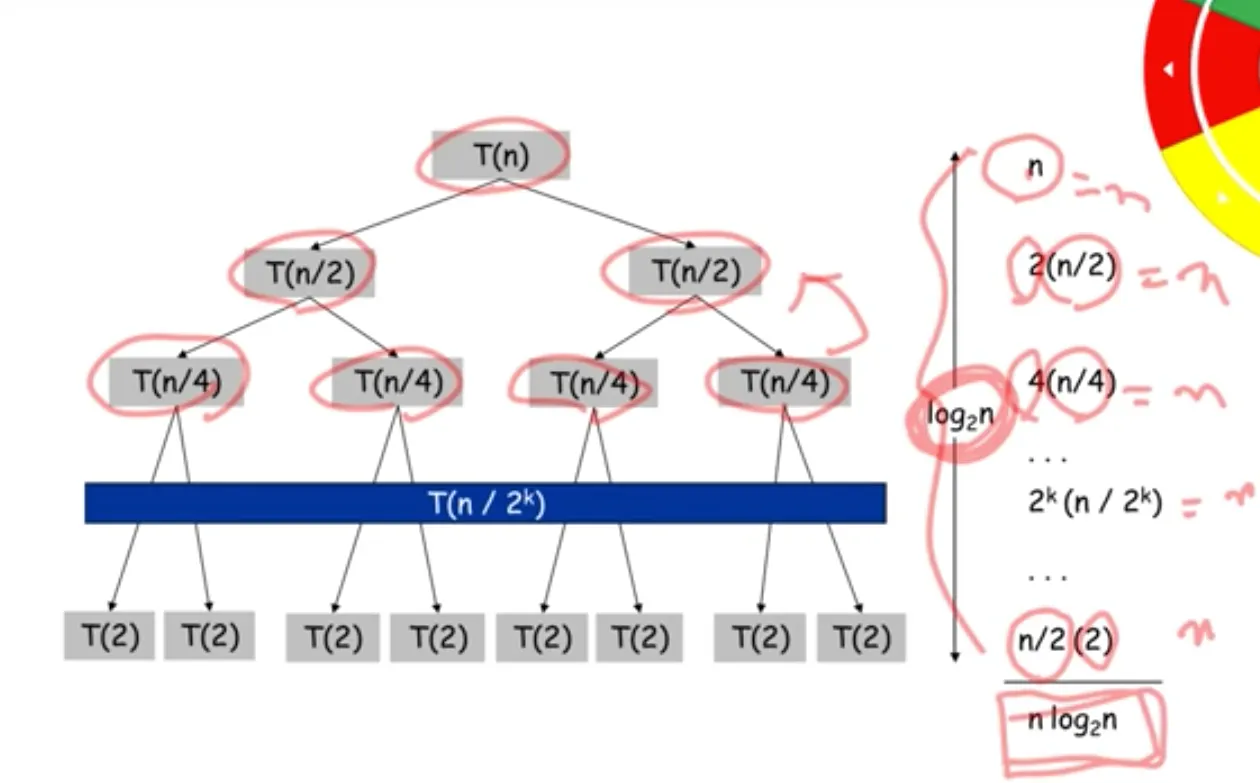
시간 복잡도
Quick Sort
분할: 특정 값을 pivot 으로 설정해서 pivot 기준으로 작은 무리, 큰 무리로 분할
정복: 순환
합병: nothing to do
•
피벗을 어떤 값으로 정하느냐에 따라서 복잡도가 달라짐. (최악은 최댓값 혹은 최솟값)
•
function quickSort (list, p, r) {
if (q < r) {
q = partition(list, p, r);
quickSort(list, p, q - 1);
quickSort(list, q + 1, r);
}
}
function partition (list, p, r) {
var pivot = list[r];
var i = p - 1;
for(var j = p; j <= r - 1; j++) {
if (list[j] <= pivot) {
i++;
swap(list[i], list[j]);
}
}
swap(list[i + 1], list[r]);
return i + 1;
}
JavaScript
복사
Partition
시간복잡도
최악의 경우
최선의 경우
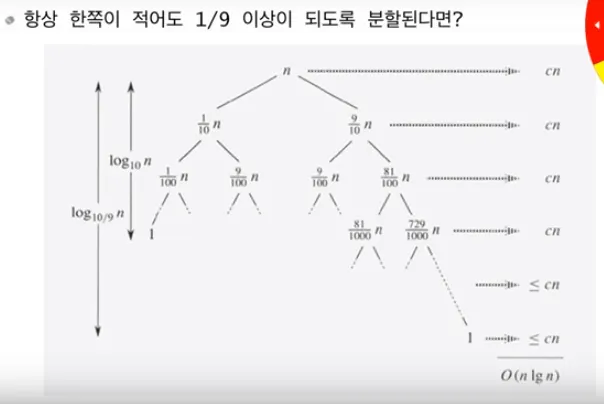
최악은 아니지만 적어도 항상 한 쪽이 1 / 9 이상이 되도록 분할할 때
•
quick sort 는 파티션이 잘 이루어 짐에 따라서 시간 복잡도가 결정된다
•
그러나 극단적인 경우(정렬된 데이터 정렬)만 아니라면 적어도 O(N logN) 이 된다
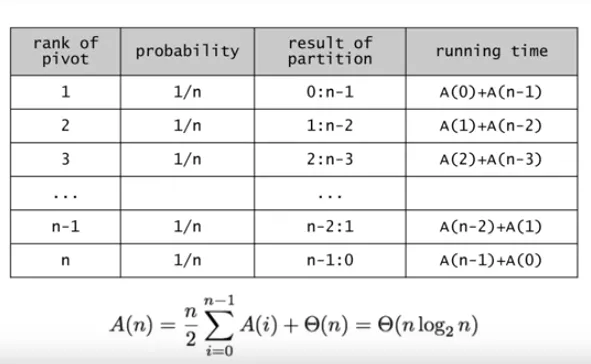
평균 시간복잡도
이미지 잘못됨. n / 2 가 아니라 2 / n 이다.
피봇 선택
•
첫번째 값이나 마지막 값을 피봇으로 선택은 별로 좋은 선택이 아니다
◦
이미 정렬된 데이터 or 역정렬 된 데이터는 최악의 경우
◦
현실의 데이터는 랜덤한 경우가 별로 없으므로 정렬된 데이터가 들어올 확률이 높음
•
Median of Three
◦
첫번째 값과 마지막 값, 그리고 가운데 값 중에서 중간값(median)을 피봇으로 선택
◦
최악의 경우 시간복잡도가 달라지지는 않음
•
Randomized Quicksort
◦
피봇을 랜덤하게 선택
◦
평균 시간복잡도 (O(NlogN))
Heap Sort
•
최악의 경우 시간복잡도 = O(n log n)
•
Sorts in place - 추가 배열 불필요 (Merge Sort 보다 좋음)
•
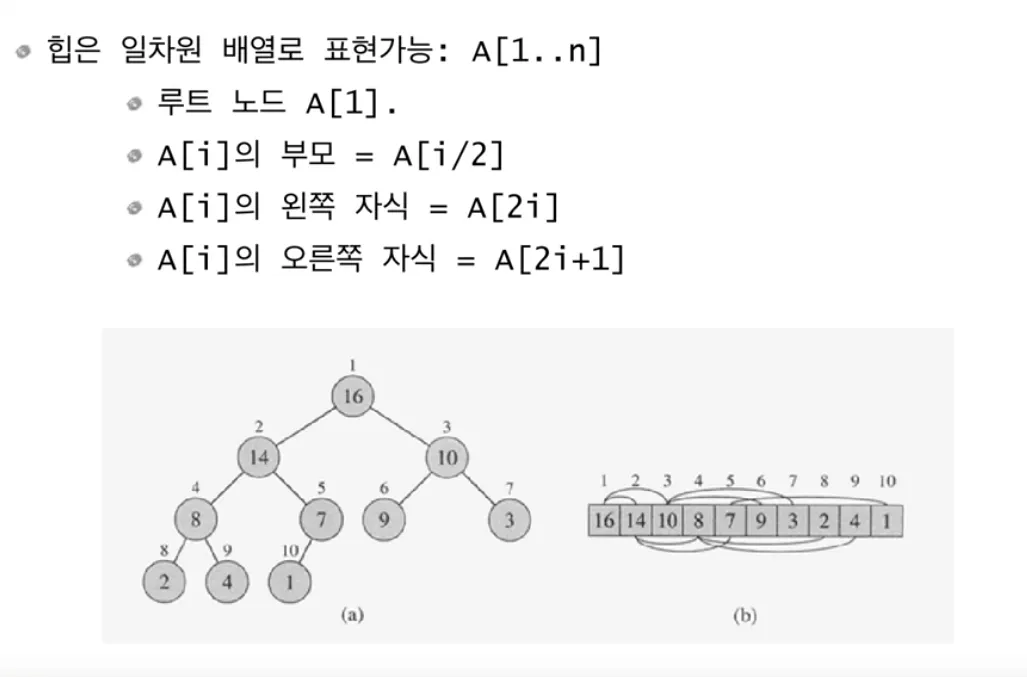
이진 힙 자료구조를 사용
•
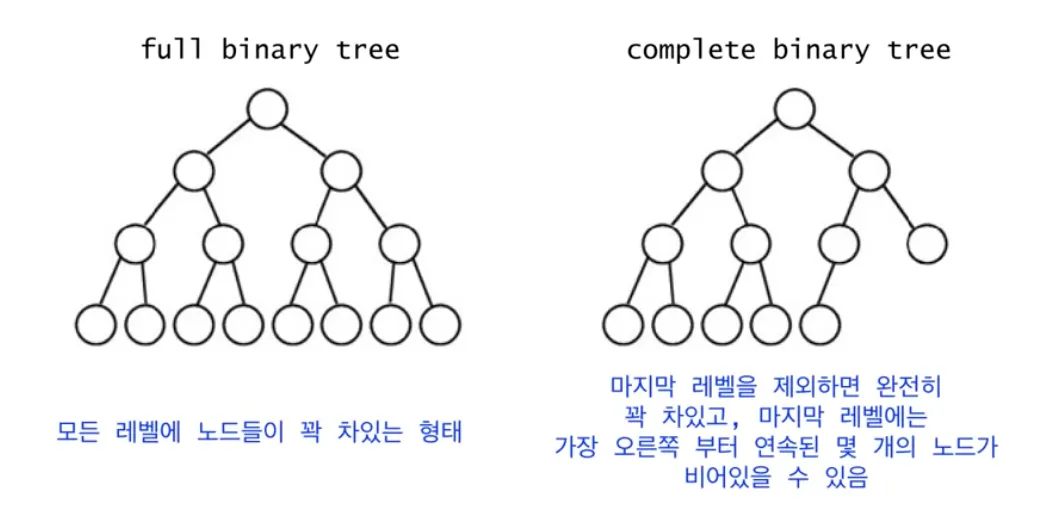
complete binary tree 이면서
•
heap propertyfmf 사용해야한다
정렬이 아니라 heap 에 만드는 시간 복잡도 !!
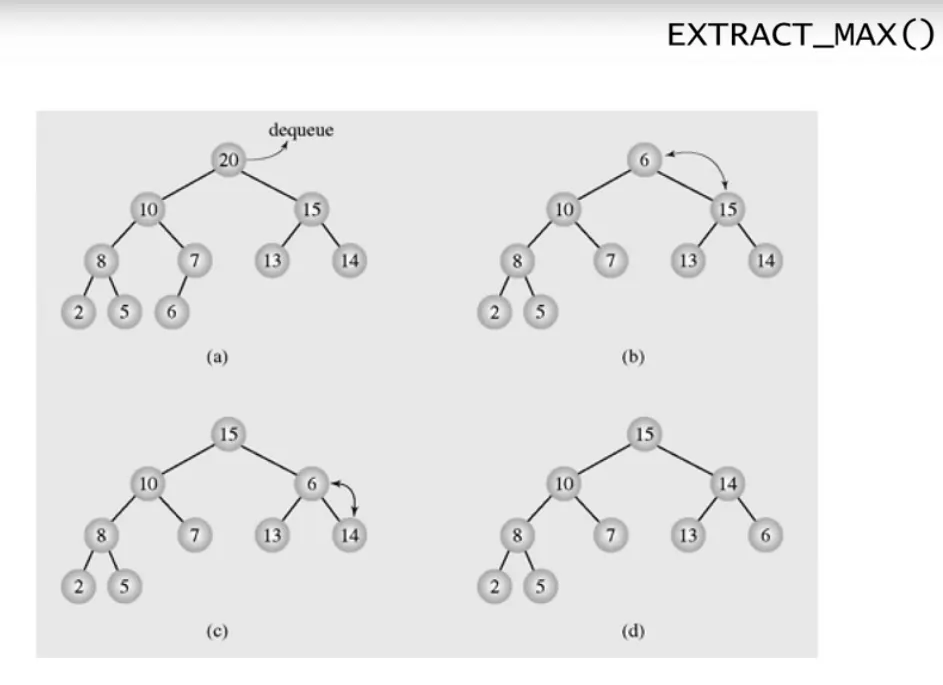
Maximum priority queue (최대 우선순위 큐)
힙 정렬의 응용
Comparison Sort 에서 최대 성능의 시간 복잡도(Lower bound)는 O(n log n)
•
입력된 데이터를 한번씩 다 보기 위해서 최소 O(n)의 시간복잡도 필요
•
합병, 힙 정렬 알고리즘들의 시간 복잡도는 O(n log n)
•
어떤 comparison sort 도 O(n log n) 보다 시간 복잡도가 낮게 나올 수 없다.
•
Leaf 노드의 갯수(가능한 정렬 갯수)는 n! 개다. (ex - n = 3 Leaf = 3 * 2 * 1)
•
최악의 경우 시간 복잡도는 트리의 높이
•
트리의 높이
height ≥ log n! = O(n log n)
Comparison sort
•
데이터들간에 상대적 크기관계만을 이용해서 정렬하는 알고리즘
•
따라서 크기 관계가 정의되어 있으면 어떤 데이터 형태든 적용 가능 (문자, 알파벳 등)
Non-comparison sort
•
정렬할 데이터에 대한 사전지식을 이용(적용에 제한)
•
ex ) Bucket sort, Radix sirt
Sorting in linear time
선형시간(O(n)) 정렬 알고리즘
데이터들을 한번만 다 보는 정도의 시간복잡도
comparison sort 가 아니다
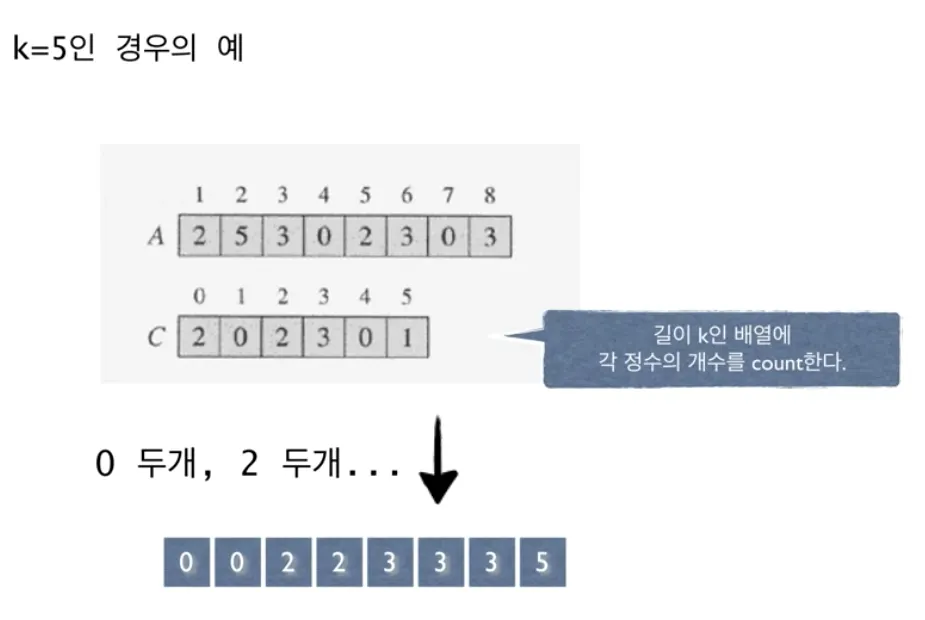
Counting Sort
•
n개의 정수를 정렬하라. 단 모든 정수는 0에서 k 사이의 정수이다.
k 가 작을 경우!
•
실제 현실에서는 이렇게 사용하기 힘들다. 왜냐하면 현실에서는 정렬을 한가지 property 만 가지지 않을 것이기 때문이다. - (ex - [{ name: 'jeff', age: 24 }, { name: 'MJ', age: 32 }])
•
k가 클 경우 비실용적 (n 보다 k 가 클 경우)
•
시간 복잡도는 O(n + k)
•
Stable 정렬 알고리즘이다
입력에 동일한 값이 있을 때 입력에 먼저 나오는 값이 출력에서도 먼저 나온다
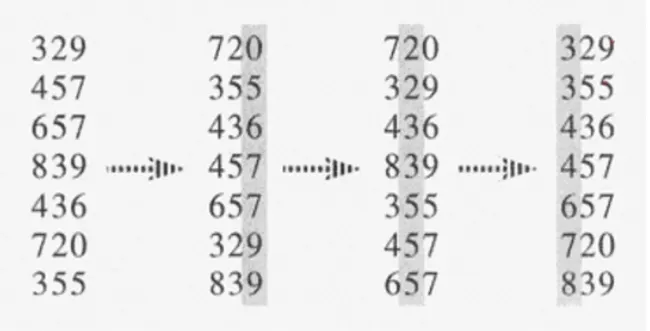
Radix sort
◦
n개의 d자리 정수들
◦
가장 낮은 자리수부터 정렬
◦
각 자리수를 정렬할 때 Stable sort 를 사용해야한다. (같은 숫자에 대해서 정렬 후 원래의 순서를 유지해야함)
시간 복잡도 = O(d(n + k))